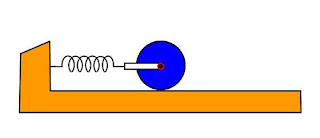
Ένας ομογενής και συμπαγής τροχός μάζας Μ=2Kg και ακτίνας R=0,25m μπορεί να περιστρέφεται χωρίς τριβές περί οριζόντιο άξονα που διέρχεται από το κέντρο του. Ο τροχός συνδέεται κατάλληλα με οριζόντιο ελατήριο, σταθεράς Κ=300Ν/m, το άλλο άκρο του οποίου έχει ακλόνητα στερεωθεί και μπορεί να κινείται πάνω σε οριζόντια επιφάνεια όπως φαίνεται στο σχήμα.. Μετακινούμε το σύστημα από την θέση ισορροπίας του κατά d=0,1m και το αφήνουμε ελεύθερο οπότε ο τροχός κυλίεται χωρίς να ολισθαίνει πάνω στην οριζόντια επιφάνεια. Δίνεται η ροπή αδράνειας του τροχού ως προς τον άξονα περιστροφής Ι=1/2ΜR2
Να υπολογίσετε:
a) Την μέγιστη τιμή της ταχύτητας του κέντρου μάζας του τροχού.
b) Την επιτάχυνση του κέντρου μάζας του τροχού σε συνάρτηση με την απομάκρυνση x από την θέση ισορροπίας του.
c) Την περίοδο των ταλαντώσεων του κέντρου μάζας του τροχού.
d) Την ελάχιστη τιμή του οριακού συντελεστή στατικής τριβής μ ώστε ο τροχός να μην ολισθαίνει.
Απάντηση:
Κύλιση και ταλάντωση
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου